덧셈 계산
@장점(편한 점)
1.작업을 동시에 하기 때문에 모든 과정을 반복하는 수고를 덜 수 있다.(소수점을 기준으로 수들을 배열한다. 소수점이 없으면 보이지 않는 소수점이 직힌 마지막 숫자를 기준으로 정렬한다.)
2.실수가 생기면 그 부분이 어디인 지 쉽게 알 수 있다.
3.계산을 처음부터 반복하지 않고도 실수를 고칠 수 있다.
규칙: 11보다 큰 숫자는 계사한하지 않는다. (계산한 총합이 11 이상일 때는 11을 뺀 나머지 값으로 다시 계산하기 시작해야 한다. 계산하다가 11보다 큰 수가 나오면 그 원래 수 옆에 ' 표시를 해준다.)
[보기]
-합산 결과와 표시줄의 두 수를 세로로 더하고, 표시줄에서 더한 그 수의 오른쪽 이웃 숫자를 더한다. 아래와 같이 하면 된다.
어떤 세로셈을 끝까지 계산하면 아래와 같다.
위의 두 줄을 더할 때는 보통 덧셈처럼 오른쪽에서 시작해서 왼쪽으로 옮겨 간다. ('ㄴ'자 모양으로 더한다.)
+더 간결하게 풀기: '11 법칙'을 사용하면 된다. 계산 결과가 11을 넘는다면, 예를 들어 계산 결과가 18이었다면 8만 남기고 거기에서 1만 빼서 7를 계산한다. 그리고 ' 표시를 한다. (십의 자리를 무시하고 일의 자리 숫자에서 1을 뺀다.)
<검산하기>
ㄱ검산은 계산할 수의 세로셈, 작업 과정, 정답의 세 요소를 활용하여 세 단계로 나뉘어 진행된다.
1단계: 계산할 수들을 세로로 적고 세로줄마다 검산 숫자를 구한다.
2단계: 작업 과정에서 검산 숫자를 구한다.
3단계: 해답(또는 합)의 검산 숫자를 구한다.
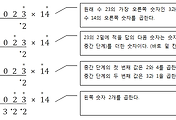
1단계: 숫자들을 세로로 계산할 때 숫자 9 혹은 더해서 9가 되는 숫자를 지우고 나머지만 계산한다. 그리고 각 자릿수를 계속 더해서 한 자릿수로 만든다. 이렇게 하여 나온 숫자가 세로줄의 검산 숫자이다.
[보기]
3 6 8 9
0 7 5 8
9 6 6 7
1 0 6 4
6 4 9 8
0 7 4 5
9 9 6 8
5 8 8 7
9 9 8 8
7 6 1 5
8 7 4 9
12 (맨 앞 첫 번째 세로줄의 나머지를 더한 결과)
3 (12의 각 자릿수를 더해서 나왔다. 1+2=3)
-지워진 숫자들을 제외한 나머지 숫자들을 더한 다음, 각 자릿수를 더한다.
위의 보기를 답과 검산 숫자를 계산하면 다음과 같다. 숫자들을 지우는 선은 밑줄 표시로 대체하여 나타냈다.
[보기2]
합산 결과: 2 3 10 1
'표시 개수: 5 6 5 7
답: 6 4 6 2 8
검산 숫자: 3 6 2 6
(9의 법칙 적용)
-검산 숫자를 한 자릿수로 만들 때, 꼭 끝까지 계산한 후 맨 마지막에 각 자릿수를 더해야 하는 것은 아니며 중간마다 더해도 된다. 게다가 이렇게 하는 편이 계산하기가 쉽다.
2단계: 이 단계에서는 작업 과정의 검산 숫자를 구한다.
[보기3]
합산 결과: 2 3 10 1
' 표시 개수: 5 6 5 7
' 표시 개수 반복: 5 6 5 7
더하기: 12 15 20 6
자릿수 합: 3 6 2 6
+검산 숫자를 구하기 위해 위와 같이 두 번째 줄(' 표시 개수)을 한 번 더 적고 모두 더한다. 첫 번째 단계의 검산 숫자들과
이번 단계에서의 결과를 비교해 보았을 때 둘 모두 3, 6, 2, 6이 나왔다. 두 결과가 일치하므로 계산이 옳음을 알 수 있다.
※만약 첫 번째 단계와 두 번째 단계의 숫자들이 일차하지 않는 상황에서는 어느 세로줄의 계산이 틀렸는지 알 수 있다. 이를테면 첫째 단계에서는 3, 6, 8, 6을 얻었고 둘째 단계에서는 3, 6, 2, 6을 얻었다고 해보자. 왼쪽에서 세 번째 숫자가 서로 다르다. 이는 왼쪽에서 세 번째 세로줄의 계산이 틀리고 나머지 세로줄의 계산은 옳다는 점을 알려준다. 세 번째 세로줄만 다시 계산하면 실수를 바로 잡을 수 있다.
3단계: 이 단계는 정답의 검산 숫자를 구하는 단계이다. 답의 검산 숫자(답의 각 자릿수의 합)를 첫 번째 단계 숫자와 두 번째 단계 숫자들과 비교하였을 때 결과가 일치하면 모든 계산이 맞았다는 것을 확인할 수 있다.
예를 들어 위의 예제에서 답은 64,628이었는데 각 자릿수를 더하여 한 자릿수로 만들면 8이다. 이 숫자를 첫 번째 단계와 두 번째 단계에서 얻은 숫자 3, 6, 2 6과 비교하면 네 숫자를 모두 더했을 때 8이 되므로 결과가 일치한다. 그러므로 모든 계산이 맞았다는 것을 확인할 수 있다.
ㄴ이 검산은 모든 덧셈에서 활용할 수 있다. 실제 계산할 때는 검산하면서 작업 과정을 다시 적을 필요가 없이 표시 개수 줄을 머릿속에서 두 번 더하면서 검산 숫자를 구하면 된다.
[보기4]
합산 결과: 2 3 10 1
'표시 개수: 5 6 5 7
답: 6 4 6 2 8
검산:
세로줄: 3 6 2 6 (9의 법칙 적용)
작업 과정: 3 6 2 6 = 8
답: 6 4 6 2 8 = 8
ㄷ또 다른 예제도 보자. 이번에는 편리하게 계산할 수 있도록 적는 방식을 약간 바꾸었다. 작업 표의 표시 개수 줄을 답 아래에 한 번 더 썼지만 작업 과정은 다시 쓰지 않았다. 정답을 제외하고 작업 과정의 이 세 줄을 더한다(합산 결과, ' 표시 개수 , ' 표시 개수).
[보기5]
0 . 8 9
0 . 2 3'
0 . 9' 6
1 . 0 4'
0 . 3' 9
0 . 2 5'
합산 결과: 1 . 2 3
'표시 개수: 0 . 2 3
합: 3 . 7 6 답은 3.76
'표시 개수 반복: 0 . 2 3
검산 숫자: 1 . 6 9
9의 법칙으로 세로줄 계산: 1 . 6 0
ㄹ이 검산에서 9의 법칙에 다라 9와 0은 같은 것으로 취급한다.
'수학 > 트라첸버그 계산법' 카테고리의 다른 글
| 트라첸버그 곱셈법 - UT곱셈법 (0) | 2016.02.20 |
|---|---|
| 트라첸버그 계산법 - 직접 곱셈법 (0) | 2016.01.29 |
| 트라첸버그 계산법 - 간단한 곱셈(5): 1부터 12까지의 곱셈 규칙 정리 (0) | 2016.01.29 |
| 트라첸버그 계산법 - 간단한 곱셈(4): 4, 3, 2, 1을 곱하는 곱셈 (0) | 2016.01.29 |
| 트라첸버그 계산법 - 간단한 곱셈(3): 8,9를 곱하는 곱셈 (0) | 2016.01.29 |



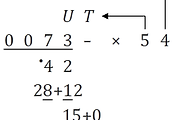

댓글